KVedaLoss provides range tables for the stopping of charged ions in a variety of solid and gaseous media. It can be used to calculated energy losses, residual energies, ranges, and the corresponding inverse calculations. It is based on the original code VEDALOSS developed by R. Dayras and E. De Filippo for the INDRA collaboration [1]. This code interpolates the range tables of Northcliffe and Schilling [2] with those of Hubert, Bimbot and Gauvin [3] in order to calculate ranges based on data valid in the energy range 0.1 ≤ E∕A ≤ 250 MeV. For E∕A < 2.5 MeV ranges are taken from [2] (which include the contribution from nuclear stopping), while at higher energies ranges are taken from [3]. It should be noted that the ranges of [3] were calculated from 2.5 MeV/nucleon upwards, taking the Northcliffe and Schilling range at 2.5 MeV/nucleon as starting point.
For each material, the interpolated range for each ion from Z = 1 to Z = 100 has been parametrised as
| (1) |
where R is the range [g∕cm2] of the ion and ϵ its incident energy [MeV /nucleon]. The six parameters ai for each atomic number Z (for a reference isotope A) were found by fitting Eq. 1 to the range data taken from [2, 3]. Ranges for different isotopes, A′, can be calculated simply using the relation
| (2) |
The range function, Eq. 1, is implemented in the code using the ROOT class TF1. In order to invert the range function and obtain the incident energy corresponding to a given range, we use method TF1::GetX().
The energy loss ΔE of a charged ion of incident energy E in a thickness Δx of a given material is calculated using
| (3) |
where R-1 is the inverse range function and ρ the density [g∕cm3] of the material. Again, this energy loss function is parametrised using ROOT::TF1, which allows to obtain incident energies from measured energy loss using TF1::GetX().
The following figures present comparisons between KVedaLoss and the original tables of [2, 3]. They are extracted from [6].
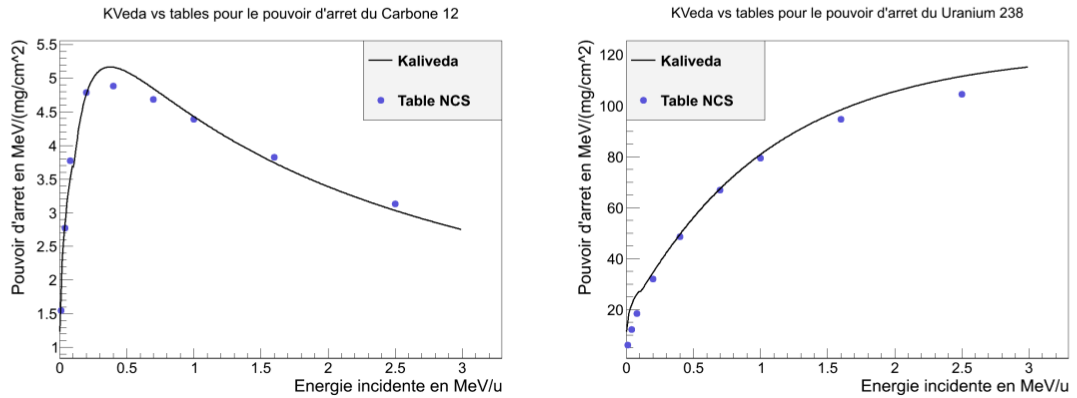
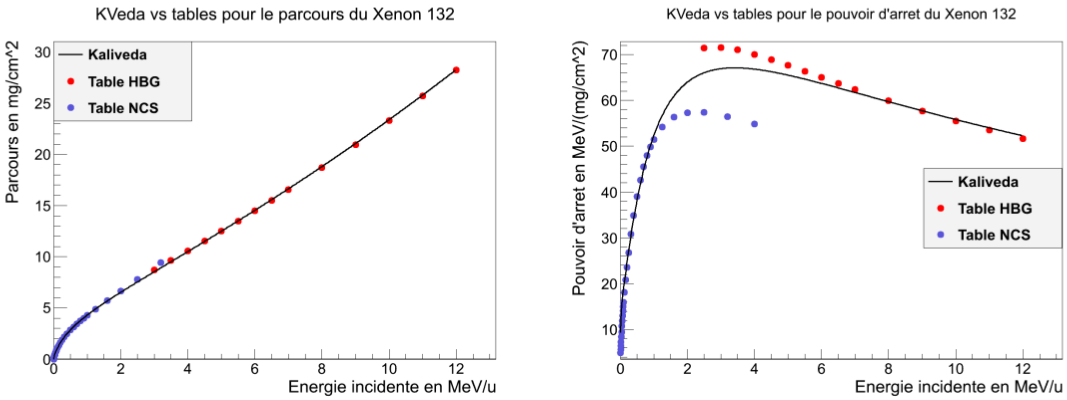
Ranges for gaseous materials were parametrised using a modified form of the ion effective charge energy dependence, using data from [4, 5]. Some comparisons between KVedaLoss and that data are presented here.
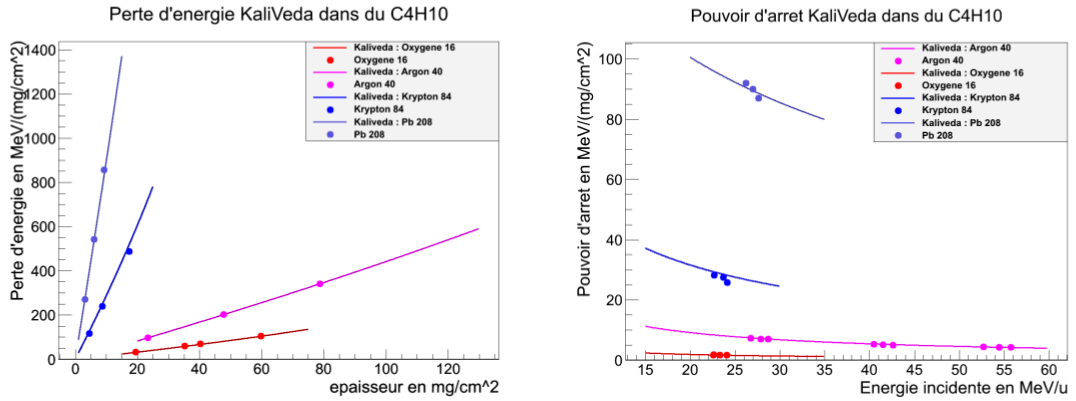
[1] R. Dayras and E. de Filippo, “Reference for the INDRA CHIO-Si identification and the Energy Loss routines”, CEA Rapport SPhN-95-60
[2] L. C. Northcliffe and R. F. Schilling, “Range and Stopping-Power Tables for Heavy Ions”, Nuclear Data Tables A7 (1970) 233
[3] F. Hubert, R. Bimbot, and H. Gauvin, “Range and Stopping-Power Tables for 2.5-500 MeV/nucleon Heavy Ions in Solids”, Atomic Data and Nuclear Data Tables 46 (1990) 1
[4] J. Herault et al., “Stopping powers of gases for heavy ions (O, Ar, Kr, Xe) at intermediate energy (20-100 MeV/u)”, Nucl. Instr. and Meth. in Phys. Research B61 (1991) 156
[5] R. Bimbot et al., “Stopping powers of gases for very heavy ions”, Nucl.Instr. and Meth. in Phys. Research B107 (1996) 9
[6] S. Cassette, Rapport de stage de deuxième année d’école d’ingénieur INPG Phelma (Grenoble), “Comparaison du pouvoir d’arrêt des ions lourds entre les simulations GEANT et un calcul analytique aux énergies de 0.1 à 250 MeV/nucléon” (2011)